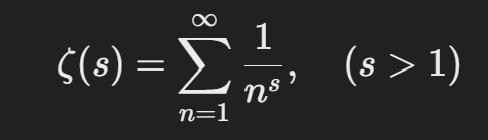1. 서론: 리만 가설이란?
리만 가설(Riemann Hypothesis)은 소수(Prime Numbers)의 분포를 설명하는 가장 중요한 문제 중 하나다.
이 가설은 **1859년 독일 수학자 베른하르트 리만(Bernhard Riemann)**이 제안했으며,
현재까지 150년 넘게 해결되지 않은 밀레니엄 7대 난제 중 하나로 남아 있다.
📌 리만 가설의 핵심 질문
“리만 제타 함수(Riemann Zeta Function)의 모든 비자명해(Non-Trivial Zero)의 실수부는 항상 1/2인가?”
이 문제가 해결되면, 소수의 분포를 더 정확히 이해할 수 있으며, 암호학, 수학, 컴퓨터 과학에 큰 영향을 미칠 것이다.
🚀 그렇다면, 리만 가설이 무엇인지 깊이 탐구하고 해결 방법을 모색해보자.
2. 리만 제타 함수(Riemann Zeta Function)란?
리만 제타 함수는 복소수 해석학에서 중요한 함수로, 소수의 분포를 분석하는 핵심 도구다.
📌 제타 함수의 정의 (실수 영역)
- 여기서 s는 실수 또는 복소수일 수 있다.
- 예를 들어, s=2이면 바젤 문제로 알려진 다음 값이 나온다:
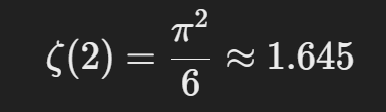
📌 복소수 확장 (리만이 제안한 형태)
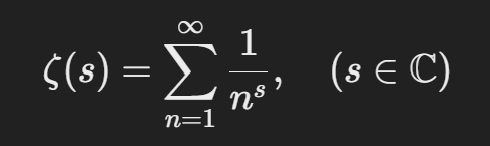
- 이 함수는 복소수 영역에서도 정의될 수 있으며, 특별한 성질을 가진다.
- 특히, 어떤 값에서 이 함수가 0이 되는지(영점, Zero)를 분석하는 것이 중요하다.
3. 리만 가설의 내용
📌 리만 가설이 주장하는 핵심 내용
“리만 제타 함수의 비자명한 제로(Non-Trivial Zeros)의 실수부는 항상 1/2”
이다.”
즉, 제타 함수가 0이 되는 중요한 지점들은 복소수 평면에서 실수부가 항상 1/2을 가진다는 것이다.
✅ 영점(Zero, 함수가 0이 되는 지점)의 분류
- 자명한 영점(Trivial Zeros): s=−2,−4,−6,−8,… (짝수 음수에서 발생)
- 비자명한 영점(Non-Trivial Zeros): 복소수 해 중 특정한 조건을 만족하는 값
💡 리만 가설이 참이라면?
- 모든 비자명한 영점은 형태가 1/2+bi(b는 실수) 와 같아야 한다.
- 즉, 복소평면에서 실수부가 항상 1/2인 특정한 수직선에 위치해야 한다.
4. 리만 가설이 중요한 이유
(1) 소수의 분포와 연관 🔢
- 소수의 개수는 무한하지만, 규칙 없이 나타나는 것처럼 보인다.
- 하지만 리만 제타 함수와 소수는 밀접한 관계가 있다.
- 리만 가설이 참이라면, 소수의 개수를 예측하는 공식(소수 정리, Prime Number Theorem)이 더욱 정교해진다.
(2) 암호학과 보안 🔐
- 현대 암호 시스템(RSA 암호 등)은 소수의 난수를 기반으로 한다.
- 만약 리만 가설이 거짓이라면, 현재의 암호 시스템이 깨질 가능성이 있음.
(3) 물리학, 양자역학과 연관 🧪
- 리만 제타 함수의 비자명한 영점은 양자역학의 에너지 준위와 비슷한 구조를 가질 수도 있다.
- 따라서 양자 물리학과 수 이론의 연결고리가 될 가능성이 있다.
5. 리만 가설 해결 방법: 가능한 접근법
💡 현재까지 수학자들이 시도한 다양한 접근법이 있지만, 결정적인 증명은 없었다.
그러나 다음과 같은 방법이 유망한 해결책이 될 수 있다.
(1) 복소 해석학과 함수 방정식 활용
- 리만 제타 함수는 특정한 대칭성(Symmetry)을 가지며, 함수 방정식을 만족한다.
- 이를 이용하여 비자명한 영점이 특정 영역에만 존재함을 증명할 수 있는가?
(2) 확률적 수학 및 랜덤 행렬 이론(Random Matrix Theory) 활용
- 물리학의 양자 혼돈 이론(Quantum Chaos)과 랜덤 행렬(Random Matrix) 연구에서
리만 제타 함수의 영점이 특정한 확률 분포를 따를 가능성이 발견됨. - 이 이론을 이용하여 비자명한 영점이 특정한 패턴을 가지는지 입증할 수 있을까?
(3) 기계 학습 및 인공지능(AI) 활용 🤖
- 현재 AI는 복잡한 수학적 패턴을 발견하는 데 사용되고 있음.
- 머신러닝을 활용하여 리만 제타 함수의 비자명한 영점이 1/2 선에 위치한다는 패턴을 학습할 수 있는가?
📌 결론: 위 방법들이 개별적으로는 성공하지 못했지만, 조합하면 강력한 해결책이 될 수도 있다!
리만 가설, 해결될 것인가?
📌 리만 가설의 핵심 정리
✅ 리만 제타 함수의 비자명한 영점의 실수부는 항상 1/2이어야 한다는 주장.
✅ 이 가설이 참이라면, 소수의 분포를 완벽히 이해할 수 있다.
✅ 암호학, 양자역학, 수 이론 등 다양한 분야에 영향을 미친다.
✅ 150년 넘게 미해결 상태이지만, 여러 접근법이 연구되고 있다.
🚀 “리만 가설이 증명되는 날, 수학과 과학의 패러다임이 바뀔 것이다!” 🔢✨
📢 “리만 가설을 해결할 다음 천재는 누구일까? 어쩌면 당신일 수도 있다!” 🏆💡