1. 서론: 수학의 심연을 들여다보는 리만 제타 함수
1859년, 독일의 수학자 **베른하르트 리만(Bernhard Riemann)**은
수학 역사상 가장 신비롭고 중요한 함수 중 하나를 연구했다.
그것이 바로 **리만 제타 함수(ζ(s))**이다.
📌 리만 제타 함수란?
\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} ]
(s가 복소수일 때 정의되는 무한급수 함수)
리만 제타 함수는 소수(Prime Number)의 분포와 직접적으로 연결되며,
수학에서 가장 난해한 문제 중 하나인 **”리만 가설(Riemann Hypothesis)”**의 핵심이다.
🚀 이 글에서는 리만 제타 함수의 정의, 그 중요성, 그리고 해결되지 않은 난제에 대해 살펴보겠다.
2. 리만 제타 함수란?
(1) 기본 정의
리만 제타 함수는 다음과 같이 정의된다:
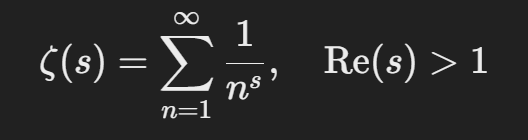
여기서 **sss**는 복소수이며, **sss의 실수 부분이 1보다 클 때 이 급수는 수렴한다.
✅ 예제:
- s=2 일 때:
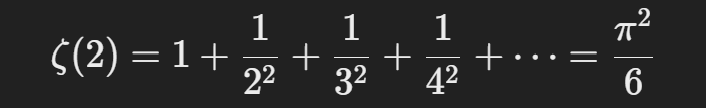
- (이 결과는 오일러가 증명한 유명한 **”바젤 문제(Basel Problem)”**의 해답이다.)
- s=1일 때:
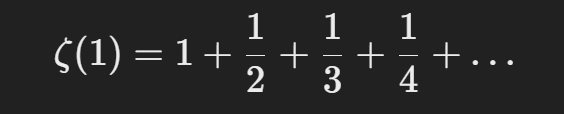
- (이 경우 급수가 발산하므로, 정의되지 않는다.)
(2) 소수와의 관계 – 오일러 곱셈 공식(Euler Product Formula)
스위스 수학자 **레온하르트 오일러(Leonhard Euler)**는
리만 제타 함수가 소수들과 밀접한 관계가 있음을 발견했다.
📌 오일러 곱셈 공식:
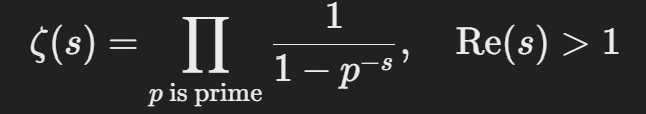
이 식은 제타 함수가 모든 소수들의 곱 형태로 표현될 수 있음을 의미한다.
즉, 제타 함수는 소수의 분포와 직접적인 연관이 있다.
✅ 의미:
- 리만 제타 함수를 연구하면, 소수들의 숨겨진 패턴을 파악할 수 있다!
- 이것이 “리만 가설”이 소수 이론에서 가장 중요한 문제로 꼽히는 이유다.
3. 리만 가설(Riemann Hypothesis) 🔥
1859년, 리만은 자신의 논문에서 제타 함수의 영점(Zero)들을 연구하면서,
아직도 풀리지 않은 수학의 가장 위대한 문제를 제시했다.
📌 리만 가설이란?
“모든 비자명한 영점(Non-trivial zero)은 실수 부분이 1/2인 형태로 존재한다.”
즉,
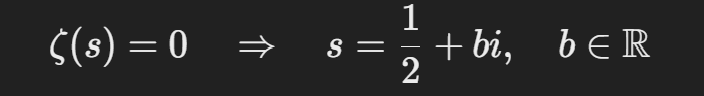
✅ 의미:
- 리만 제타 함수는 특정한 값에서 0이 된다.
- 이 값들(영점)이 실수 부분이 1/2인 복소수 형태로 정렬된다면,
소수의 분포가 일정한 패턴을 가진다는 사실이 증명된다.
📌 왜 중요한가?
- 소수는 무작위적으로 퍼져 있는 것처럼 보이지만, 사실은 일정한 패턴을 가진다.
- 리만 가설이 참이라면, 소수들의 분포를 정확히 예측할 수 있다.
- 현대 암호학, 난수 생성, 양자 컴퓨팅에도 영향을 미친다.
4. 리만 가설이 풀리지 않은 이유
(1) 10^13개의 영점이 1/2선 위에 있다! 하지만…
- 컴퓨터로 계산한 결과, 1000조 개 이상의 영점이 모두 실수 부분이 1/2인 형태를 가진다.
- 하지만 모든 경우에 대해 참이라는 것을 수학적으로 증명하지 못했다.
(2) 밀레니엄 문제 – 100만 달러의 상금
- **2000년, 클레이 수학 연구소(Clay Mathematics Institute)**는
**”리만 가설을 증명하는 사람에게 100만 달러를 지급하겠다”**고 발표했다. - 하지만 여전히 수학자들은 이 문제를 해결하지 못하고 있다.
📌 리만 가설이 증명된다면?
- 소수의 분포를 정확히 이해할 수 있으며, 현대 수학의 기초가 완성된다.
- 하지만 만약 거짓이라면?
- 현대 수학의 기초 이론이 흔들리고, 암호학과 난수 생성 이론도 영향을 받게 된다.
5. 현대 수학에서의 응용과 연구 방향
(1) 암호학(Cryptography)과 보안
- RSA 암호화는 소수의 곱을 이용한 보안 기법이다.
- 리만 가설이 증명되면, 소수 분해가 더 쉬워질 수도 있어 암호 체계가 바뀌어야 할 수도 있다.
(2) 양자 컴퓨터와 소수 이론
- 양자 컴퓨터가 발전하면서 소수 분해 속도가 빨라지고 있다.
- 만약 리만 가설이 증명된다면, 양자 컴퓨터를 활용한 새로운 암호 체계가 등장할 가능성이 크다.
(3) 난수 생성과 금융 수학
- 난수(random number)와 소수의 관계는 금융 모델, AI 학습 등에 필수적이다.
- 리만 가설이 참이라면, 더 효율적인 난수 생성 알고리즘이 개발될 수 있다.
6. 결론: 수학계의 마지막 미스터리
📌 리만 제타 함수는 단순한 수학적 개념이 아니다.
- 소수의 비밀을 밝히는 열쇠이며,
- 암호학, 금융, AI, 물리학 등 다양한 분야에 영향을 미친다.
📌 리만 가설은 아직도 미해결 상태이며,
- 수학계에서 가장 중요한 난제 중 하나다.
- 누군가 이를 증명한다면, 100만 달러의 상금을 받을 뿐만 아니라, 인류 역사에 길이 남을 것이다.
🚀 “소수의 패턴을 이해하는 것은, 우주의 비밀을 푸는 것과 같다.
리만 제타 함수는 그 열쇠를 쥐고 있는 가장 중요한 함수다!” 🔢✨
